|
Section 1: Forces and motion
|
a) Units
1.1: Use the following units: kilogram (kg), meter (m), meter per second (m/s), meter/second² (m/s²), newton (N), second (s), newton per kilogram (N/kg), kilogram meter per second (kg m/s)
Kilogram: Used to measure mass
Meter: Used to measure distance
Meter per second: Used to measure distance in a given period of time
Meter per second squared: Used to measure acceleration
Newton: Used to measure force
Second: Used to measure time
Newton per kilogram: Used to measure force per unit of mass
Kilogram meter per second: Used to measure momentum
Kilogram: Used to measure mass
Meter: Used to measure distance
Meter per second: Used to measure distance in a given period of time
Meter per second squared: Used to measure acceleration
Newton: Used to measure force
Second: Used to measure time
Newton per kilogram: Used to measure force per unit of mass
Kilogram meter per second: Used to measure momentum
b) Movement and position
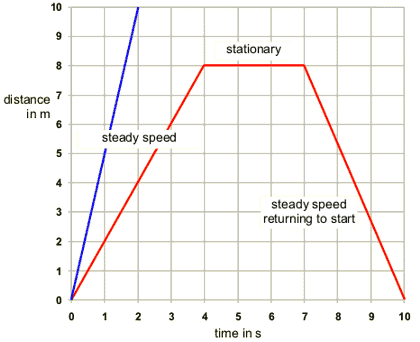
1.2: Plot and interpret distance-time graphs
1.3: Know and use the relationship between average speed, distance moved, and time taken
Average Speed = distance moved / time taken
Time Taken = distance moved / average speed
Distance Moved = average speed x time taken
Average Speed = distance moved / time taken
Time Taken = distance moved / average speed
Distance Moved = average speed x time taken
1.4: Describe experiments to investigate the motion of everyday objects such as toy cars or tennis balls
- Use a tennis ball machine to periodically shoot tennis balls
- Measure how far the tennis balls go and how long it takes them
- Use the relationship between average speed, distance moved and time taken to measure the average speed of the tennis balls
1.5: Know and use the relationship between acceleration, velocity and time
Acceleration = change in velocity / time taken
a = (v - u) / t
Acceleration = change in velocity / time taken
a = (v - u) / t
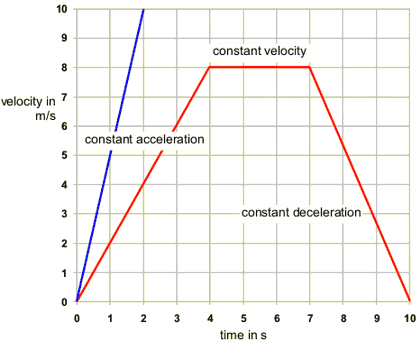
1.6: Plot and interpret velocity-time graphs
1.7: Determine acceleration from the gradient of a velocity-time graph
The steeper the gradient, the more rapidly the velocity is changing. If the graph has an upward gradient, the object is accelerating. If the graph has a downward gradient, the object is decelerating.
The steeper the gradient, the more rapidly the velocity is changing. If the graph has an upward gradient, the object is accelerating. If the graph has a downward gradient, the object is decelerating.
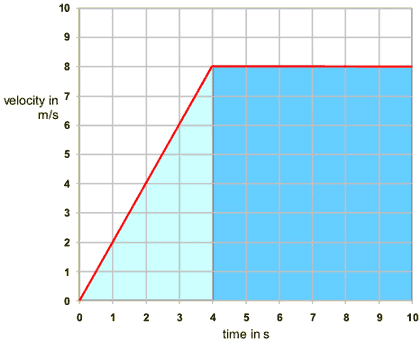
1.8: Determine the distance travelled from the area between a velocity-time graph and the time axis
The area under the line in a velocity-time graph represents the distance travelled by the object. In order to calculate the distance travelled:
The area under the line in a velocity-time graph represents the distance travelled by the object. In order to calculate the distance travelled:
- Split the area under the line into rectangles and triangles
- Calculate the area of the of the shapes
- Make sure you calculate the area of all the shapes in the graph
- Add all of their areas together in order to calculate the distance travelled
Forces, movement, shape and momentum
1.9: Describe the effects of forces between bodies such as changes in speed, shape or direction
Changes in speed
When an object is stationary, it has an equal upwards and downwards force, the upwards force being the force being exerted upon the object by the surface it is on and the downwards force being gravity. When an object is accelerating, it still has the upwards and downwards forces, but the forward force is larger than the backwards force. When the speed of an object is constant, the forward and backward forces are equal. When an object is decelerating, the backward force is larger, making the object slow down.
Changes in shape
Changes in shape effect the momentum of the object. This is shown by the equation:
Force = change in momentum / time taken
The above relationship can be proven using crumple zones in cars.
Changes in direction
The direction that the object travels in is dependent on whichever direction the force is greatest towards.
Changes in speed
When an object is stationary, it has an equal upwards and downwards force, the upwards force being the force being exerted upon the object by the surface it is on and the downwards force being gravity. When an object is accelerating, it still has the upwards and downwards forces, but the forward force is larger than the backwards force. When the speed of an object is constant, the forward and backward forces are equal. When an object is decelerating, the backward force is larger, making the object slow down.
Changes in shape
Changes in shape effect the momentum of the object. This is shown by the equation:
Force = change in momentum / time taken
The above relationship can be proven using crumple zones in cars.
Changes in direction
The direction that the object travels in is dependent on whichever direction the force is greatest towards.
1.10: Identify different types of forces such as gravitational or electrostatic
There are several different types of forces including:
There are several different types of forces including:
- Gravitational
- Electrostatic
- Magnetic
- Contact forces (push and pull)
1.11: Distinguish between vector and scalar quantities
- Vector quantities have size/magnitude and direction
- Scalar quantities have size/magnitude only
1.12: Understand that force is a vector quantity
Force is a vector quantity - it has size and direction.
Force is a vector quantity - it has size and direction.
1.13: Find the resultant force of forces that act along a line
1.14: Understand that friction is a force that opposes motion
Friction is a force which always opposes motion.
Friction is a force which always opposes motion.
1.15: Know and use the relationship between unbalanced force, mass and acceleration
Force = mass x acceleration
F = m x a
"May the force be equal to mass times acceleration"
"May the mass times acceleration be with you"
Force = mass x acceleration
F = m x a
"May the force be equal to mass times acceleration"
"May the mass times acceleration be with you"
1.16: Know and use the relationship between weight, mass, and g
Weight = mass x g
W = m x g
Weight = mass x g
W = m x g
1.17: Describe the forces acting on falling objects and explain why falling objects reach a terminal velocity
While an object is falling, it has air resistance and gravity acting upon it. When air resistance and gravity become equal, the object falls at terminal velocity. Terminal velocity is when the acceleration of the object is constant; it no longer speeds up.
While an object is falling, it has air resistance and gravity acting upon it. When air resistance and gravity become equal, the object falls at terminal velocity. Terminal velocity is when the acceleration of the object is constant; it no longer speeds up.
1.18: Describe experiments to investigate the forces acting on falling objects, such as sycamore seeds or parachutes
- Dropping a parachute from a given height shows that gravity is acting upon it
- By increasing the surface area of the parachute, it is revealed that the air resistance increases as the surface area increases
1.19: Describe the factors affecting vehicle stopping distance
Speed
The faster the speed of the vehicle, the larger the stopping distance
Mass
The larger the mass of the vehicle, the larger the stopping distance
Road Condition
There are different road conditions that can affect stopping distance in different ways. For example, ice on the road will reduce friction which will increase stopping distance
Reaction Time
The longer the reaction time, the larger the stopping distance
Speed
The faster the speed of the vehicle, the larger the stopping distance
Mass
The larger the mass of the vehicle, the larger the stopping distance
Road Condition
There are different road conditions that can affect stopping distance in different ways. For example, ice on the road will reduce friction which will increase stopping distance
Reaction Time
The longer the reaction time, the larger the stopping distance
1.20: Know and use the relationship between momentum, mass and velocity
Momentum = mass x velocity
p = m x v
Momentum = mass x velocity
p = m x v
1.21: Use the idea of momentum to explain safety measures
Car crumple zones use momentum to their advantage. If a car crashes into a wall without a crumple zone, it is in contact with the wall for a much shorter period of time than if it had a crumple zone. For example:
Without a crumple zone
50,000 kg m/s → 0 kg m/s in 0.1 seconds
Force on passengers = 500,000 N
With a crumple zone
50,000 kg m/s → 0 kg m/s in 2 seconds
Force on passengers = 25,000 N
Car crumple zones use momentum to their advantage. If a car crashes into a wall without a crumple zone, it is in contact with the wall for a much shorter period of time than if it had a crumple zone. For example:
Without a crumple zone
50,000 kg m/s → 0 kg m/s in 0.1 seconds
Force on passengers = 500,000 N
With a crumple zone
50,000 kg m/s → 0 kg m/s in 2 seconds
Force on passengers = 25,000 N
1.22: Use the conservation of momentum to calculate the mass, velocity or momentum on objects
p = m x v
m = p / v
v = p / m
p = m x v
m = p / v
v = p / m
1.23: Know and use the relationship between force, change in momentum and time taken
Force = change in momentum / time taken
Force = change in momentum / time taken
1.24: Demonstrate an understanding of Newton's third law
Newton's Third Law of Motion:
Every action has an equal and opposite reaction
Newton's Third Law of Motion:
Every action has an equal and opposite reaction
1.25: Know and use the relationship between the moment of a force and its distance from the pivot
Moment = force x perpendicular distance from pivot
Moment = force x perpendicular distance from pivot
1.26: Recall that the weight of a body acts through its center of gravity
The weight of a body acts through its center of gravity
The weight of a body acts through its center of gravity
1.27: Know and use the principle of moments for a simple system of parallel forces acting in one plane
You should be able to manipulate the moments equation in order to answer questions related to forces acting upon a straight line.
Moment = force x perpendicular distance from pivot
Perpendicular distance from pivot = moment / force
Force = moment / perpendicular distance from pivot
You should be able to manipulate the moments equation in order to answer questions related to forces acting upon a straight line.
Moment = force x perpendicular distance from pivot
Perpendicular distance from pivot = moment / force
Force = moment / perpendicular distance from pivot
1.28: Understand that the upward forces on a light beam, supported at its ends, vary with the position of a heavy object placed on the beam
Upward forces on a light beam (a ruler), that is supported on its ends, vary with the position of a weight on the beam. For example, if there is an object exerting a force of 600 N in the center of the beam, the upward forces on either side of the beam will be 300 N each
Upward forces on a light beam (a ruler), that is supported on its ends, vary with the position of a weight on the beam. For example, if there is an object exerting a force of 600 N in the center of the beam, the upward forces on either side of the beam will be 300 N each
|
1.29: Describe experiments to investigate how extension varies with applied force for helical springs, metal wires and rubber bands
|
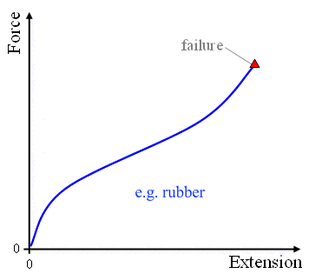
1.30: Understand that the initial linear region of a force-extension graph is associated with Hooke's law
A force-extension graph shows how much a material stretches in proportion to the force applied. The initial linear region is a straight diagonal line - it shows that the force and extension increase at the same rate. When the graph begins to curve, it shows that the material has reached its elastic potential.
A force-extension graph shows how much a material stretches in proportion to the force applied. The initial linear region is a straight diagonal line - it shows that the force and extension increase at the same rate. When the graph begins to curve, it shows that the material has reached its elastic potential.
1.31: Describe elastic behavior as the ability of a material to recover its original shape after the forces causing deformation have been removed
All different types of plastic retain their original shape after the force of deformation has been eliminated. For example, if you stretch a rubber band then let go, it will bounce back to its original dimensions.
All different types of plastic retain their original shape after the force of deformation has been eliminated. For example, if you stretch a rubber band then let go, it will bounce back to its original dimensions.
d) Astronomy
1.32: Understand gravitational field strength, g, and recall that it is different on other planets and the moon from that on the Earth
The gravitational field strength on each planet is different. g is the force that the planet is exerting on you to pull you towards the core of the planet. For example, if Earth is exerting 10 N of force on you, you will not be able to jump as high as you would be able to on a planet where g is equal to 6 N.
The gravitational field strength on each planet is different. g is the force that the planet is exerting on you to pull you towards the core of the planet. For example, if Earth is exerting 10 N of force on you, you will not be able to jump as high as you would be able to on a planet where g is equal to 6 N.
1.33: Explain the causes of gravitational force
- Gravitational force causes moons to orbit planets
- Gravitational force causes planets to orbit their Sun
- Gravitational force causes satellites to orbit the Earth
- Gravitational force causes comets to orbit the Sun
1.34: Describe the differences in the orbits of comets, moons and planets
Moons
• Orbit planets
• Slightly elliptical or near-circular orbits
• Near constant orbital speed
Planets
• Orbit stars
• Slightly elliptical or near-circular orbits
• Near constant orbital speed
Comets
• Orbit stars
• Highly elliptical or very irregular orbits
• Eccentric orbital speed
Moons
• Orbit planets
• Slightly elliptical or near-circular orbits
• Near constant orbital speed
Planets
• Orbit stars
• Slightly elliptical or near-circular orbits
• Near constant orbital speed
Comets
• Orbit stars
• Highly elliptical or very irregular orbits
• Eccentric orbital speed
1.35: Use the relationship between orbital speed, orbital radius and time period
Orbital speed = (2 x π x orbital radius) / time period
v = (2 x π x r) / T
Orbital speed = (2 x π x orbital radius) / time period
v = (2 x π x r) / T
1.36: Understand facts about the size of the universe
- The universe is a collection of billions of galaxies
- A galaxy consists of many solar systems
- Our solar system is a part of the Milky Way galaxy