|
Section 5: Solids, liquids and gases
|
a) Units
5.1: Use the following units: degrees Celsius (°C), kelvin (K), joule (J), kilogram (kg), kilogram/meter3, meter (m), meter2 (m2), meter3 (m3), meter/second (m/s), meter/second2 (m/s2), newton (N), pascal (Pa)
Celsius: Used to measure temperature
Kelvin: Used to measure temperature
Joule: Used to measure amount of energy
Kilogram: Used to measure mass
Kilogram per meter cubed: Used to measure density
Meter: Used to measure distance
Meter squared: Used to measure area
Meter cubed: Used to measure volume
Meter per second: Used to measure distance in a given period of time
Meter per second squared: Used to measure acceleration
Newton: Used to measure force
Pascal: Used to measure pressure
Kelvin: Used to measure temperature
Joule: Used to measure amount of energy
Kilogram: Used to measure mass
Kilogram per meter cubed: Used to measure density
Meter: Used to measure distance
Meter squared: Used to measure area
Meter cubed: Used to measure volume
Meter per second: Used to measure distance in a given period of time
Meter per second squared: Used to measure acceleration
Newton: Used to measure force
Pascal: Used to measure pressure
b) Density and pressure
5.2: Know and use the relationship between density, mass and volume
Density = mass / volume
ρ = M / V
Density = mass / volume
ρ = M / V
5.3: Describe experiments to determine density using direct measurements of mass and volume
Regular objects
Irregular objects
Regular objects
- Measure the mass of the object using a balance
- Measure the volume of the regular object using the length, width and height
- Use the relationship between mass, volume and density to calculate the density of the object
Irregular objects
- Measure the mass of the object using a balance
- Measure the volume of the irregular object by fully immersing it in water and measuring the displacement of the water in order to calculate the density of the object
5.4: Know and use the relationship between pressure, force and area
Pressure = force / area
p = F / A
Pressure = force / area
p = F / A
5.5: Understand that the pressure at a point in a gas or liquid which is at rest acts equally in all directions
Pressure in liquids acts equally in all directions as long as the liquid is not moving. This can easily be demonstrated using a can of water with holes punched in the bottom. Gases also exert pressure on things around them. This pressure may vary if the gas is moving, but if it is immobile the pressure acts equally in all directions.
Pressure in liquids acts equally in all directions as long as the liquid is not moving. This can easily be demonstrated using a can of water with holes punched in the bottom. Gases also exert pressure on things around them. This pressure may vary if the gas is moving, but if it is immobile the pressure acts equally in all directions.
5.6: Know and use the relationship for pressure difference
Pressure difference = height x density x g
p = h x ρ x g
Pressure difference = height x density x g
p = h x ρ x g
c) Change of state
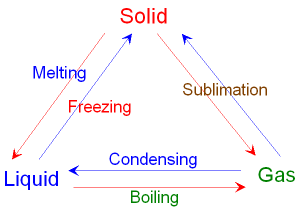
5.7: Understand the changes that occur when a solid melts to form a liquid, and when a liquid evaporates or boils to form a gas
5.8: Describe the arrangement and motion of particles in solids, liquids and gases
|
Property
spacing of particles pattern forces between particles definite shape easily compressible relative density can flow (fluid) expands to fill container |
Solids
very close regular pattern very strong yes no high no no |
Liquids
very close random strong no no high yes no |
Gases
far apart random weak no yes low yes yes |
d) Ideal gas molecules
5.9: Understand the significance of Brownian motion, as supporting evidence for particle theory
An observation by Scottish botanist Robert Brown shows that tiny non-living particles in water move in a similar way to pollen grains: they appear to jerk about in random movements. This supports the theory that all substances are made from particles, that is, particle theory. It showed that particles in a fluid (liquid or gas) are continuously moving around and bumping into each other. Sometimes there will be more or less collisions than others, so the speed and direction of particles will change.
An observation by Scottish botanist Robert Brown shows that tiny non-living particles in water move in a similar way to pollen grains: they appear to jerk about in random movements. This supports the theory that all substances are made from particles, that is, particle theory. It showed that particles in a fluid (liquid or gas) are continuously moving around and bumping into each other. Sometimes there will be more or less collisions than others, so the speed and direction of particles will change.
5.10: Understand that molecules in a gas have a random motion and that they exert a force and hence a pressure on the walls of the container
Gases are made up of constantly moving particles. These particles are spread out and they move in a random, haphazard way. Gases can be compressed into containers because these particles are so spread out. When a gas is squashed into a smaller container, it presses on the walls of the container with a greater pressure. However, this only happens when the temperature is kept the same, because a change in temperature leads to a change in kinetic energy. If the same number of particles are squeezed into a smaller volume, there will be more collisions between the gas particles and the walls of the container, more force will be exerted on the walls of the container. More average collisions per unit of time means that a greater force is exerted, and therefore a greater pressure.
Gases are made up of constantly moving particles. These particles are spread out and they move in a random, haphazard way. Gases can be compressed into containers because these particles are so spread out. When a gas is squashed into a smaller container, it presses on the walls of the container with a greater pressure. However, this only happens when the temperature is kept the same, because a change in temperature leads to a change in kinetic energy. If the same number of particles are squeezed into a smaller volume, there will be more collisions between the gas particles and the walls of the container, more force will be exerted on the walls of the container. More average collisions per unit of time means that a greater force is exerted, and therefore a greater pressure.
5.11: Understand why there is an absolute zero of temperature which is -273°C
As gas is cooled, the pressure it exerts decreases. The pressure cannot become less than zero, so this suggests that there is a temperature at which it is not possible to cool gas any further. This temperature is called absolute zero and experiments show that this is -273°C.
As gas is cooled, the pressure it exerts decreases. The pressure cannot become less than zero, so this suggests that there is a temperature at which it is not possible to cool gas any further. This temperature is called absolute zero and experiments show that this is -273°C.
5.12: Describe the kelvin scale of temperature and be able to convert between the Kelvin and Celsius scales
The kelvin temperature scale starts from absolute zero, so zero kelvin is -273°C. The kelvin temperature of a gas is proportional to the average kinetic energy of its molecules. It is possible to convert between the Kelvin and Celsius scales:
The kelvin temperature scale starts from absolute zero, so zero kelvin is -273°C. The kelvin temperature of a gas is proportional to the average kinetic energy of its molecules. It is possible to convert between the Kelvin and Celsius scales:
- temperature in K = temperature in °C + 273
- temperature in °C = temperature in K - 273
5.13: Understand that an increase in temperature results in an increase in the average speed of gas molecules
When a constant volume of gas is heated, the particles of gas continue to move randomly, but with a higher average speed since the increase in temperature provides them with more kinetic energy.
When a constant volume of gas is heated, the particles of gas continue to move randomly, but with a higher average speed since the increase in temperature provides them with more kinetic energy.
5.14: Understand that the Kelvin temperature of the gas is proportional to the average kinetic energy of its molecules
The numbers on the Kelvin temperature scale are proportional to the average kinetic energy of the molecules in a gas. The higher the number on the Kelvin scale, the higher the average kinetic energy of the gas molecules.
The numbers on the Kelvin temperature scale are proportional to the average kinetic energy of the molecules in a gas. The higher the number on the Kelvin scale, the higher the average kinetic energy of the gas molecules.
5.15: Describe the qualitative relationship between pressure and Kelvin temperature for a gas in a sealed container
If a graph of pressure is drawn using the kelvin temperature scale, a graph is created with a straight line passing through the origin. This shows that the pressure of a gas is proportional to its kelvin temperature. For example, if a gas is heated from 200K to 400K, its pressure will double.
If a graph of pressure is drawn using the kelvin temperature scale, a graph is created with a straight line passing through the origin. This shows that the pressure of a gas is proportional to its kelvin temperature. For example, if a gas is heated from 200K to 400K, its pressure will double.
5.16: Use the relationship between the pressure and Kelvin temperature of a fixed mass of gas at constant volume
Pressure and temperature in Kelvin can be calculated using the following equation:
P1 / T1 = P2 / T2
Pressure and temperature in Kelvin can be calculated using the following equation:
P1 / T1 = P2 / T2
5.17: Use the relationship between the pressure and volume of a fixed mass of gas at constant temperature
Pressure and volume of a gas at a constant temperature can be calculated using the following equation:
P1V1 = P2V2
Pressure and volume of a gas at a constant temperature can be calculated using the following equation:
P1V1 = P2V2